leetcode-x的平方根

点击：题目链接：实现 int sqrt(int x) 函数。
计算并返回 x 的平方根，其中 x 是非负整数。
由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去

思路

首先我们可以使用二分法，范围可以是0到所给的数，然后使中间数的平方不断找到最接近的那个值

代码

class Solution {
public:
    int mySqrt(int x) {
        int l = 0, r = x, ans = -1;

        while(l<=r){
            int mid = (r+l)/2;
            
            if((long long)mid*mid <=x){
                ans = mid;
                l = mid+1;
            }
            else{
                r = mid-1;
            }
        }
        return ans;
    }
};

复杂度

时间：O（logN）, 空间O（1）

思路

还有一种就是使用牛顿迭代法。假设x为我们要找的数，C为给的目标值，那么x²无限接近于C。那我们列出这么一个二元一次方程，y= x²-C。当y=0时，即满足所需条件。
我们任取一个值，（x0,x0²-C），然后取该点的切线斜率（二次方程求导）2x, 由此可得切线方程，y= 2x*x0 + x0²-C,

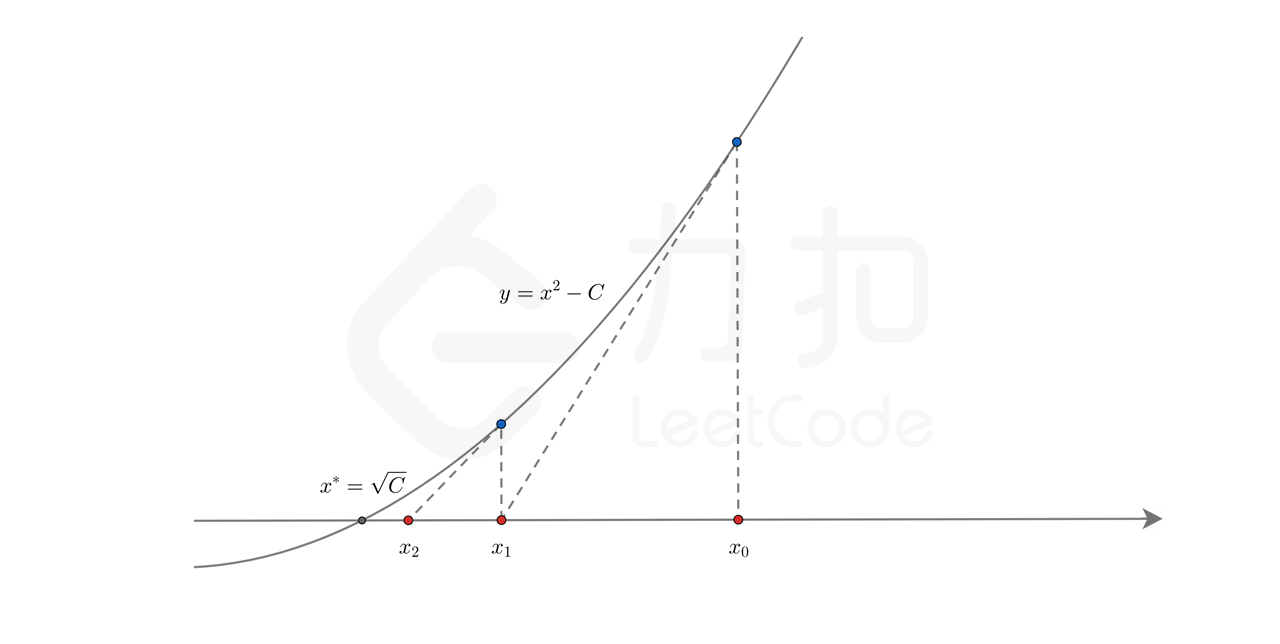
由图我们看到当x0的切线与x轴相交时，就是我们下一个迭代点。即2x*x0 + x0²-C中x的值就是下一个我们所要用的迭代点。当两个点不断接近时，理论上来说该点就是我们所要的开平方数。一般两个点差值小于等于-10的六次方到七次方,就可以满足条件了

class Solution {
public:
    int mySqrt(int x) {
        if(x==0) return x;

        double x0 = x, C= x, xi = -1;
        while(true){
            xi = 0.5*(x0+ C/x0);
            if(fabs(x0-xi) <1e-7){
                break;
            }
            x0 = xi;
        }
        return x0;
    }
};

复杂度

时间：O（logX）,比二分法更快一些。空间：O（1）

拓展

若要保留小数点后几位，可以先乘10的几次方，然后再除以它

参考

num =(int) (num * 1000);
num = (double)(num / 1000);